Deep learning
An introduction for the layperson
Giorgio Sironi - SETI@eLife

(if you're reading this on your laptop, press S for notes)
Giorgio Sironi (@giorgiosironi)






We propose that a 2 month, 10 man study of artificial intelligence be carried out during the summer of 1956 at Dartmouth College in Hanover, New Hampshire. The study is to proceed on the basis of the conjecture that every aspect of learning or any other feature of intelligence can in principle be so precisely described that a machine can be made to simulate it. An attempt will be made to find how to make machines use language, form abstractions and concepts, solve kinds of problems now reserved for humans, and improve themselves. We think that a significant advance can be made in one or more of these problems if a carefully selected group of scientists work on it together for a summer.
John McCarthy (LISP), Claude Shannon (information theory), Marvin Minsky et al, 1956
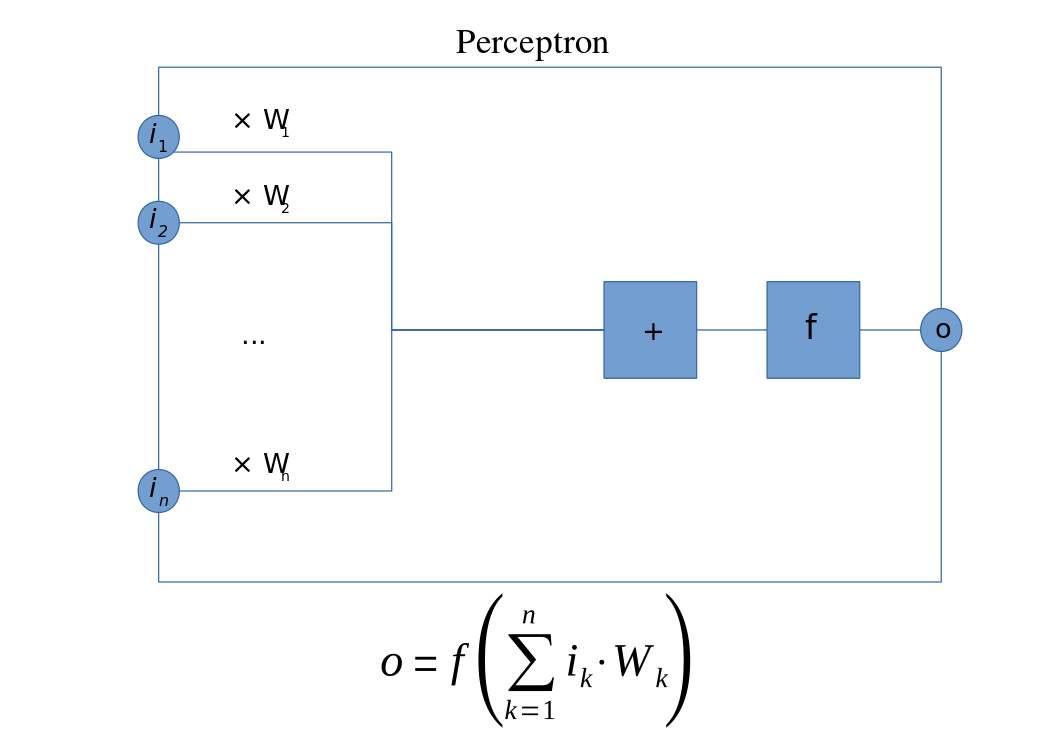
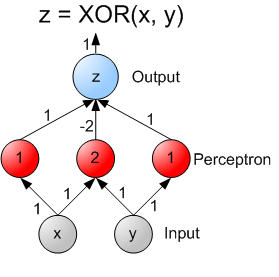
| x1 | x2 | ŷ | y | e |
|---|---|---|---|---|
| 0 | 0 | 0 | -0.1 | 0.1 |
| 0 | 1 | 0 | 0.2 | -0.2 |
| 1 | 0 | 0 | 1.1 | -1.1 |
| 1 | 1 | 1 | 0.9 | 0.1 |
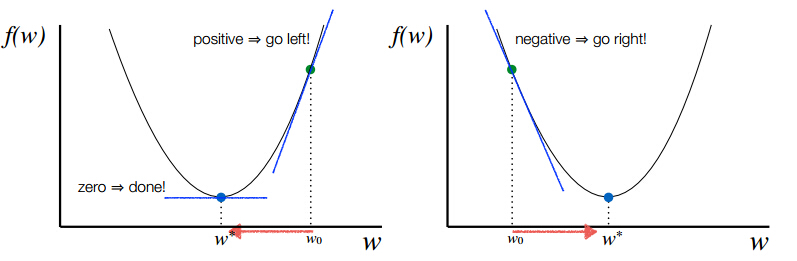
for each example x:
y = f(w * x) // * is a vector product
e = ŷ - y // + error, - derivative
for each weight i:
wi = η * e * xi // ∝ derivative
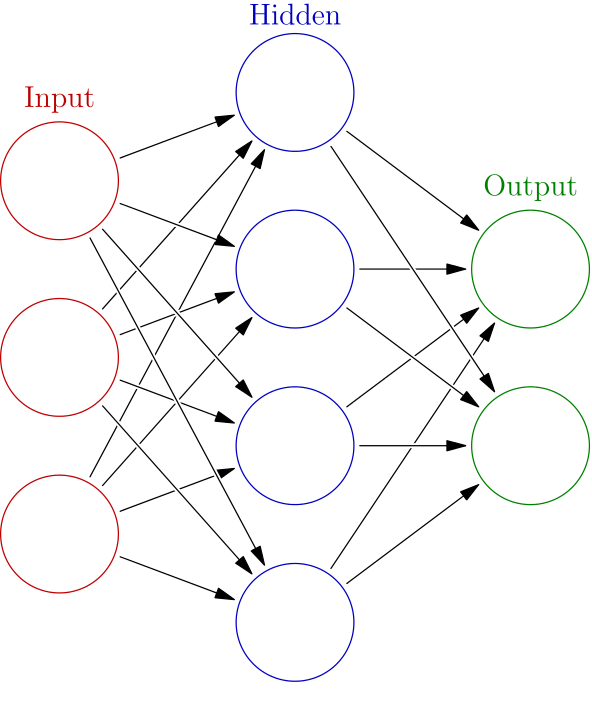
In from three to eight years we will have a machine with the general intelligence of an average human being. -- Marvin Minsky, 1970
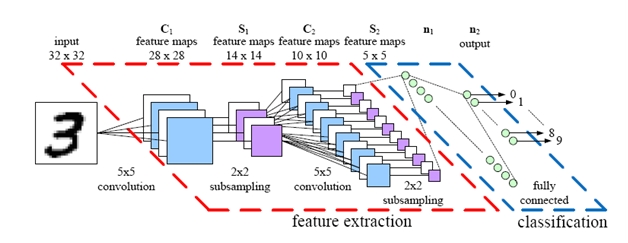
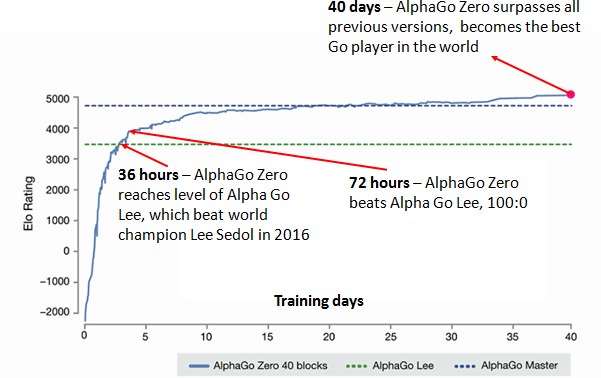
On training set: This data set contains 29.4 million positions from 160,000 games played by KGS 6 to 9 dan human players
On training time and resources: The value network was trained for 50 million mini-batches of 32 positions, using 50 GPUs, for one week.